SBMPTN Zone : Kubus

Berikut ini adalah kumpulan soal memgenai Kubus tingkat SBMPTN. Jika ada jawaban yang salah, mohon dikoreksi melalui komentar. Terima kasih.
Tingkat kesulitan :

• Tingkat kesulitan 👉
• Dasar
• SBMPTN
• Olimpiade

---

No. 1

Diketahui suatu kubus ABCD.EFGH memiliki panjang sisi a cm. Titik P berada di rusuk AB sehingga {AP:PB=1:3}, titik Q berada di rusuk BC sehingga {BQ:QC=3:1}, titik R berada di rusuk BF sehingga {BR:RF=3:1}. Jika \alpha adalah sudut antara bidang PQR dan garis DR, maka nilai \tan\alpha= ....

1. \dfrac{5\sqrt2}{14}
2. \dfrac{14}{\sqrt{246}}
3. \dfrac{7\sqrt{246}}{123}

4. \dfrac{\sqrt{246}}{14}
5. \dfrac12\sqrt2

DB=a\sqrt2
OB=\dfrac12DB=\dfrac12a\sqrt2

OS:SB=AP:PB=1:3

\(\eqalign{ SB&=\dfrac3{1+3}OB\\ &=\dfrac34\left(\dfrac12a\sqrt2\right)\\ &=\dfrac38a\sqrt2 }\)

BR=\dfrac34a

\(\eqalign{ \tan\alpha&=\tan\left(\angle BRD-\angle BRS\right)\\ &=\dfrac{\tan\angle BRD-\tan\angle BRS}{1+\tan\angle BRD\tan\angle BRS}\\ &=\dfrac{\dfrac{DB}{BR}-\dfrac{SB}{BR}}{1+\dfrac{DB}{BR}\cdot\dfrac{SB}{BR}}\\ &=\dfrac{\dfrac{a\sqrt2}{\dfrac34a}-\dfrac{\dfrac38a\sqrt2}{\dfrac34a}}{1+\dfrac{a\sqrt2}{\dfrac34a}\cdot\dfrac{\dfrac38a\sqrt2}{\dfrac34a}}\\ &=\dfrac{\dfrac43\sqrt2-\dfrac12\sqrt2}{1+\dfrac43\sqrt2\cdot\dfrac12\sqrt2}\\ &=\dfrac{\dfrac56\sqrt2}{1+\dfrac43}\\ &=\dfrac{\dfrac56\sqrt2}{\dfrac73}\cdot\dfrac66\\ &=\dfrac{5\sqrt2}{14} }\)

JAWAB: A

---

No. 2

Diketahui kubus ABCD.EFGH dengan panjang rusuk 2\sqrt2 cm. Jika P di tengah-tengah AB dan titik Q di tengah-tengah BC, maka jarak titik H dengan garis PQ adalah ... cm.

1. \sqrt{15}
2. 4
3. \sqrt{17}

4. 3\sqrt2
5. >\sqrt{19}

SBMPTN 2018

Hubungkan titik H dan titik P, hubungkan titik H dan titik Q. Segitiga HPQ merupakan segitiga sama kaki sehingga jarak titik H ke garis PQ adalah panjang garis dari titik H ke tengah garis PQ. Misal titik tengah PQ adalah titik R.
{AP=PB=BQ=\dfrac12\left(2\sqrt2\right)=\sqrt2}

{PQ=\sqrt2\cdot\sqrt2=2}

\(\eqalign{ PR&=\dfrac12PQ\\ &=\dfrac12(2)\\ &=1 }\)

HA=2\sqrt2\cdot\sqrt2=4

\(\eqalign{ HP&=\sqrt{HA^2+AP^2}\\ &=\sqrt{4^2+\left(\sqrt2\right)^2}\\ &=\sqrt{16+4}\\ &=\sqrt{20} }\)

\(\eqalign{ HR&=\sqrt{HP^2-PR^2}\\ &=\sqrt{\left(\sqrt{20}\right)^2-1^2}\\ &=\sqrt{20-1}\\ &=\boxed{\boxed{\sqrt{19}}} }\)

Jadi, jarak titik H dengan garis PQ adalah \sqrt{19} cm
JAWAB: E

---

No. 3

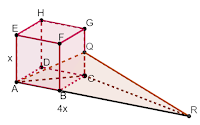
Sebuah kubus ABCD.EFGH memiliki panjang rusuk x. Q adalah titik tengah dari rusuk GC, dan R adalah perpanjangan garis AB sehingga {AB + BR = AR = 4x}. Maka, perbandingan volume limas Q.ARC dan volume kubus ABCD.EFGH adalah

1. 1:1
2. 1:2
3. 2:1

4. 3:1
5. 1:3

t=CQ=\dfrac12x

\(\begin{aligned} L_a&=L_{ARC}\\ &=\dfrac12\cdot AR\cdot BC\\ &=\dfrac12\cdot4x\cdot x\\ &=2x^2 \end{aligned}\)

\(\begin{aligned} V_{Q.ARC}&=\dfrac13L_at\\ &=\dfrac13\cdot2x^2\cdot\dfrac12x\\ &=\dfrac13x^3\\ \end{aligned}\)

\(\begin{aligned} \dfrac{v_{Q.ARC}}{V_{ABCD.EFGH}}&=\dfrac{\dfrac13x^3}{x^3}\\ &=\dfrac13\\ &=1:3 \end{aligned}\)

Jadi, perbandingan volume limas Q.ARC dan volume kubus ABCD.EFGH adalah 1:3.
JAWAB: E

---

No. 4

Pada kubus ABCD.EFGH, P pada EG sehingga {EP:PG=1:2}. Jika jarak E ke garis AP adalah a, maka panjang rusuk kubus tersebut adalah

1. \dfrac{a}{11}\sqrt2
2. \dfrac{a}2\sqrt{11}
3. a\sqrt{22}

4. \dfrac{a}2\sqrt{22}
5. a\sqrt{11}

Misal jarak E ke AP adalah EQ=a, dan panjang rusuknya adalah s.

\(\begin{aligned} AP&=\sqrt{s^2+\left(\dfrac13s\sqrt2\right)^2}\\ &=\sqrt{s^2+\dfrac29s^2}\\ &=\sqrt{\dfrac{11}9s^2}\\ &=\dfrac{s}3\sqrt{11} \end{aligned}\)

\(\begin{aligned} EQ&=\dfrac{AE\cdot EP}{AP}\\[8pt] a&=\dfrac{s\cdot \dfrac{s}3}{\dfrac{s}3\sqrt{11}}\\[15pt] &=\dfrac{s}{\sqrt{11}}\\ s&=\boxed{\boxed{a\sqrt{11}}} \end{aligned}\)

Jadi, panjang rusuk kubus tersebut adalah a\sqrt{11}.
JAWAB: E

Share this post